Marking my 10th article, I figured I should take it back to the start of my blog, only this time I’ll be solving a leetcode hard

Problem Statement

The imbalance number of a 0-indexed integer array arr of length n is defined as the number of indices in sarr = sorted(arr) such that:

• 0 <= i < n - 1, and
• sarr[i+1] - sarr[i] > 1

Here, sorted(arr) is the function that returns the sorted version of arr.

Given a 0-indexed integer array nums, return the sum of imbalance numbers of all its subarrays.

A subarray is a contiguous non-empty sequence of elements within an array.

Constraints:

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= nums.length

Naive Approach

Let’s say you have three integers a, b and c, where a < b < c. It goes without saying, the subarray of (a, c) has an imbalance of 1

a < b < c   <=>   c > b > a
b > a       <=>   b >= a + 1
c > b       <=>   c >= b + 1
c > b > a   <=>   c >= a + 2

c - a >= 2 > 1
c - a > 1

Now let’s add b to our subarray (a, c)

Since a < b < c, we can replace the imbalance of (a, c) with (a, b) and add a new group called (b, c) to our subarray

This is more of a convenient way to visualize things

Since we know the imbalance of (a, c) is 1, if b - a <= 1 we subtract 1 from the total imbalance of the subarray, and if b - a > 1 we do nothing, as 1 had already been added to the subarray when it was only (a, c)

On the other end, if c - b > 1 we add 1 to our subarray and if c - b <= 0 we do nothing, as initially this second group didn’t exist

Now we’ve found a convenient way to add new numbers to existing subarrays

But there are three edge cases

Let’s call the new number num

Edge Case 1

What if num is less than every number in the subarray? What if there’s no nice way to slip it into the existing sub array?

Let’s just add it to the start

So in the event there’s a sub array with distinct integers (s1, s2, s3, s4...). If num is less than every number in the sub array, adding num to the subarray results in this (num, s1, s2, s3, s4...) in this case, the new total imbalance will be the imbalance of existing subarray + s1 - num > 1 ? 1 : 0

Edge Case 2

Similary, if num is greater than every number in the subarray, the new total imbalance would be imbalance of existing subarray + sn - num > 1 ? 1 : 0 where sn is the last number in the sub array

Edge Case 3

What if we put in a number that’s not distinct? A number that’s already spoken for?

Like adding 5 to this subarray (1, 2, 5, 6), in this case, we do nothing

There’s no need to do anything as the imbalance does not change, 5 - 5 is 0 and 5 - 2, 6 - 5 have already been spoken for

When all is said and done here’s how the solution looks like

/**
 * @param {number[]} nums
 * @return {number}
 */

var sumImbalanceNumbers = function(nums) {
  let ans = 0
  for(let i = 0; i < nums.length-1; i++){
    const set = new Set([nums[i]])
    let max = nums[i], min = nums[i], imbalance = 0
    for(let j = i+1; j < nums.length; j++){
      // Ignore non distinct num
      if(!set.has(nums[j])){
        // Edge Case 2
        if(max < nums[j]){
          if(nums[j] > max+1)imbalance++
          max = nums[j]
        // Edge Case 1
        }else if(min > nums[j]){
          if(nums[j] < min-1)imbalance++
          min = nums[j]
        }else{
          // b - a
          if(set.has(nums[j]-1))imbalance--
          // c - b
          if(!set.has(nums[j]+1))imbalance++
        }
        set.add(nums[j])
      }
      ans += imbalance
    }
  }
  return ans
};

Improvement

We’ve solved the hard problem, but I don’t know, maybe it’s the double loop talking but it feels empty

Let’s look for ways we can improve it

Cooking

If you noticed, in the code, we didn’t really look for the number at the front or behind num, all we did was check if there’s a num + 1 or num - 1

We did that because, firstly, we ignored repeat num, and secondly, if there isn’t a num + 1 that would mean the number after it has at least a difference of 2

if sx > num and sx !== num + 1 then sx >= num + 2

Similarily, for the number behind num, checking if it’s num - 1 suffices for our problem

But… do we really need to check what’s behind?

Let’s say we have a subarray (a, b, c) where a < b < c, previously we had b check both a and c but what if a checks with b and b checks with c, it’s the same on paper, only this time sx/num is only in charge of the number in front of it

But to do that, we’ll need to know what a, b and c are, and we’re currently only finding them out through a for loop

Oh wait, we only need to know if a + 1 and b + 1 exist

…that’s feasible

Using dp and preprocessing we could…

const N = nums.length
const lastIndex = new Map()
const rightEdge = new Array(N)
for (let i = N - 1; i >= 0; i--) {
  const num = nums[i]
  rightEdge[i] = lastIndex.get(num + 1) ?? N
  lastIndex.set(num, i)
}

With this we get the last time num + 1 existed on the right side of the array

That means any number before the lastIndex does not have num + 1, nice!

What about the left side?

We could do something similar

const N = nums.length
const lastIndex = new Map()
const leftEdge = new Array(N)
for (let i = 0; i < N; i++) {
  const num = nums[i]
  leftEdge[i] = lastIndex.get(num + 1) ?? N
  lastIndex.set(num, i)
}

So we have a way to know the range, both left and right of num where num + 1 does not exist, the total imbalance num can create will be how many ways we can permutate the left and right ranges since we already know any permutation would be valid

/**
 * @param {number[]} nums
 * @return {number}
 */

var sumImbalanceNumbers = function(nums) {
  const N = nums.length

  const lastIndex = new Map()
  // right side
  const rightEdge = new Array(N)
  for (let i = N - 1; i >= 0; i--) {
    const num = nums[i]
    rightEdge[i] = lastIndex.get(num + 1) ?? N
    lastIndex.set(num, i)
  }

  let count = 0

  lastIndex.clear()
  for (let i = 0; i < N; i++) {
    const num = nums[i]
    // left side
    const leftEdge = lastIndex.get(num + 1) ?? -1
    // permutation
    count += (i - leftEdge) * (rightEdge[i] - i)
    lastIndex.set(num, i)
  }
  return count
}

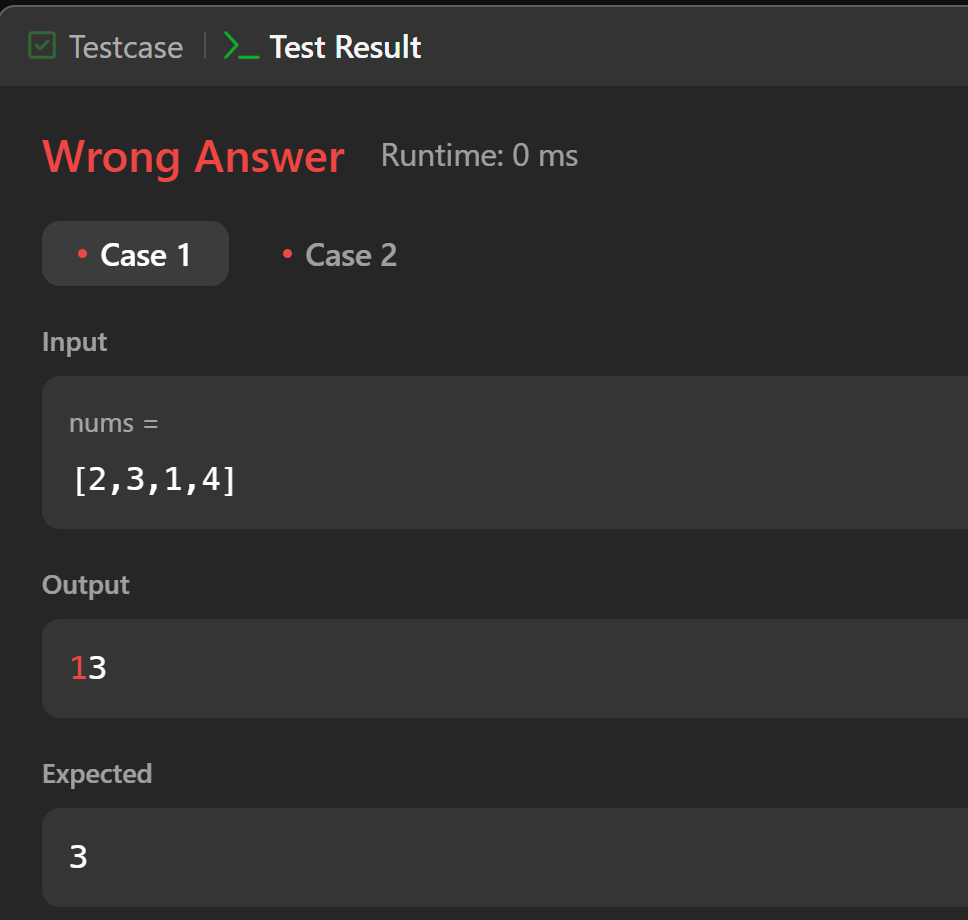
Hmmm

Oh right!

Our initial solution ignored repeat num but this one lets it go through, that means if there’s a 5 in the sub array, another 5 adds to the imbalance instead of being ignored

Since we’re only considering the right side, that just means we have to account for both num + 1 and num at the right side

const N = nums.length
const lastIndex = new Map()
const rightEdge = new Array(N)
for (let i = N - 1; i >= 0; i--) {
  const num = nums[i]
  // num + 1 and num accounted for (as things to ignore)
  rightEdge[i] = Math.min(lastIndex.get(num + 1) ?? N, lastIndex.get(num) ?? N)
  lastIndex.set(num, i)
}

Hmmm

What else?

…oh

We accounted for a - b and b - c, but we also account for c - null. We checked the right side of every element in the sub array including the last element, and if there was no sx and sx + 1 we added 1 to the total imbalance

Since every sub array has a last element, we’ll need to subtract one, from every sub array

The total number of subarrays in an array of length N is N * (N + 1) / 2

Think of it this way, given an array of length N, there is one way of creating a sub array of length N, two for length N - 1, three for length N - 2…, N for length 1

Adding it all together gives you N * (N + 1) / 2

And subtracting it from our total gives us this beauty

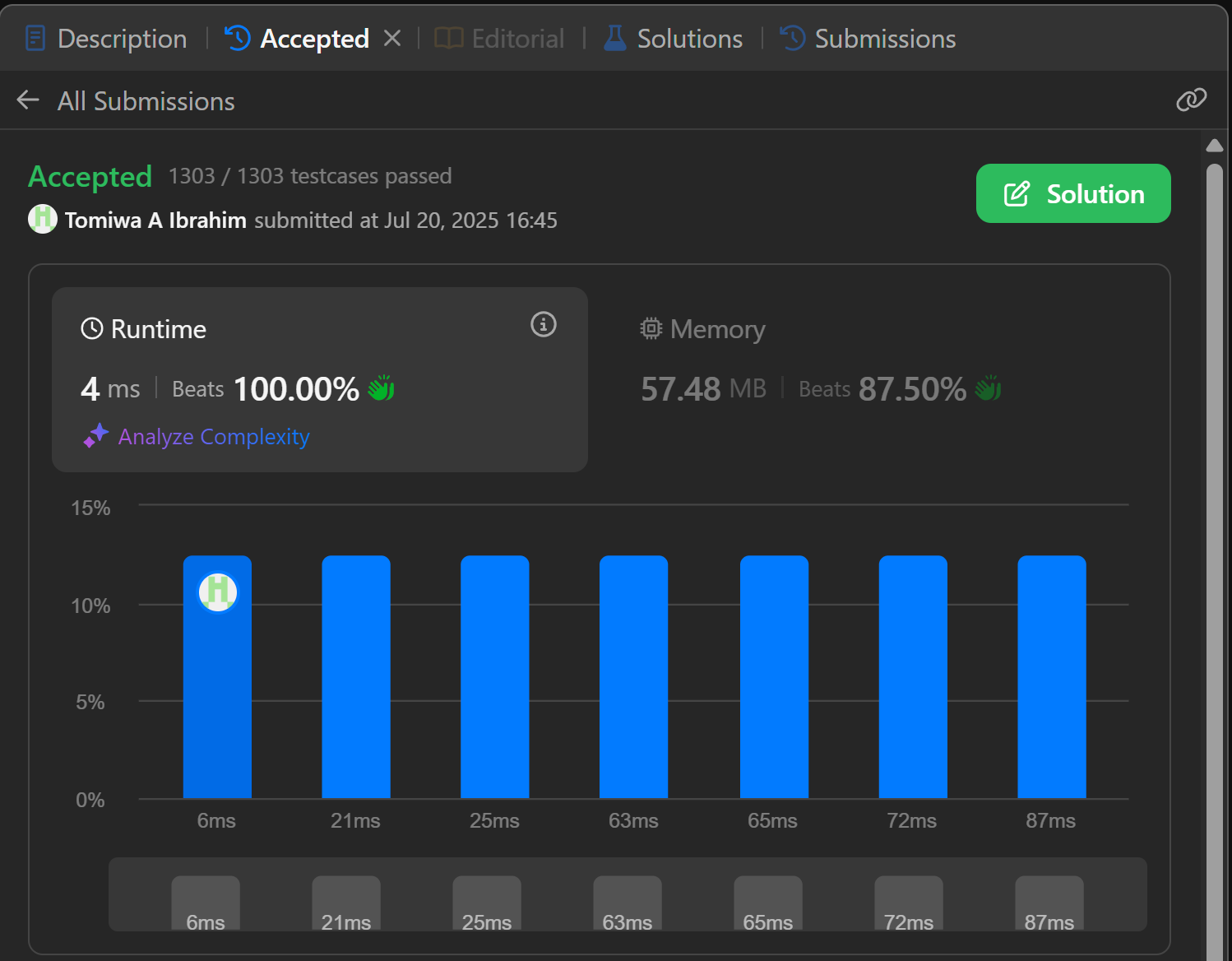
We aren’t done yet!

If you look closely at the constraint you’ll see something

• 1 <= nums[i] <= nums.length

That means, lastIndex has a definite length it can be, since we know what the maximum value num could be

const lastIndex = new Map()

const lastIndex = new Array(N + 2)

that leads us to this beauty

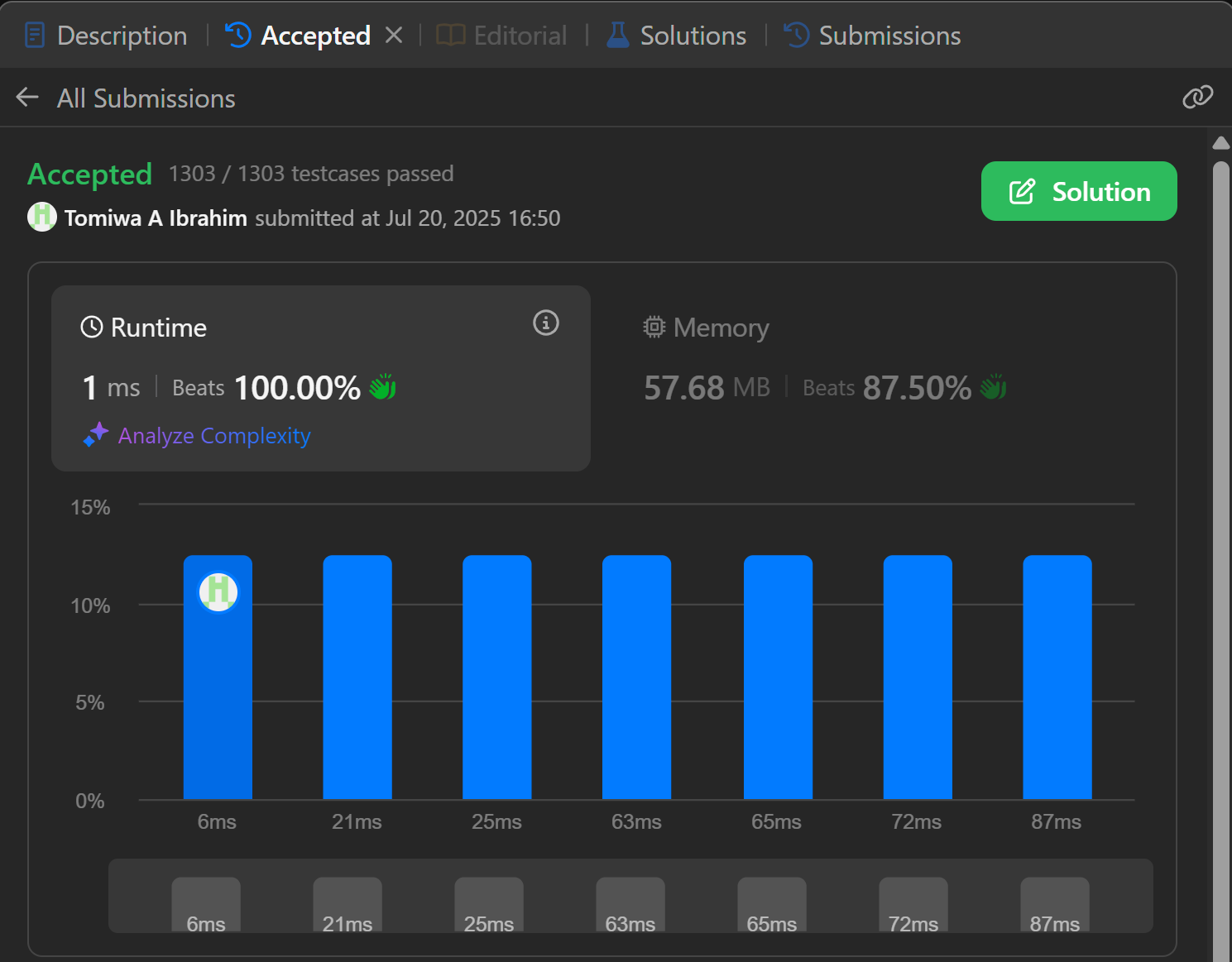
Author’s Note

Here’s the final code

var sumImbalanceNumbers = function(nums) {
  const N = nums.length

  const lastIndex = new Array(N + 2).fill(N)
  const rightEdge = new Array(N)
  for (let i = N - 1; i >= 0; i--) {
    const num = nums[i]
    rightEdge[i] =  Math.min(lastIndex[num + 1], lastIndex[num])
    lastIndex[num] = i
  }

  let count = 0

  lastIndex.fill(-1)
  for (let i = 0; i < N; i++) {
    const num = nums[i]
    const leftEdge = lastIndex[num + 1]
    count += (i - leftEdge) * (rightEdge[i] - i)
    lastIndex[num] = i
  }
  return count - N * (N + 1) / 2
}

And here’s the submission link

It was a fun problem